kinematics multiple choice questions and answers
Time Left: 45:00
Total Marks: 80, Obtained Marks: 0
1. A particle is projected up the incline such that its component of velocity along the incline is \(10 \, \text{m/s}\). Time of flight is \(2 \, \text{seconds}\) and maximum height above the incline is \(5 \, \text{m}\). Then, velocity of projection will be:
A. \(10 \, \text{m/s}\)
B. \(10 \sqrt{2} \, \text{m/s}\)
C. \(5 \sqrt{5} \, \text{m/s}\)
D. None
Explanation:
Given the time of flight \(T = 2 \, \text{seconds}\) and maximum height above the incline \(H = 5 \, \text{m}\):
The component of the velocity along the incline \(v_{\text{incline}} = 10 \, \text{m/s}\). The formula for time of flight is: \[ T = \frac{2u \sin \theta}{g_{\text{eff}}} \] and for maximum height: \[ H = \frac{u^2 \sin^2 \theta}{2g_{\text{eff}}}. \] Using the data and solving these equations, we find that the velocity of projection \(u = 10 \sqrt{2} \, \text{m/s}\).
Given the time of flight \(T = 2 \, \text{seconds}\) and maximum height above the incline \(H = 5 \, \text{m}\):
The component of the velocity along the incline \(v_{\text{incline}} = 10 \, \text{m/s}\). The formula for time of flight is: \[ T = \frac{2u \sin \theta}{g_{\text{eff}}} \] and for maximum height: \[ H = \frac{u^2 \sin^2 \theta}{2g_{\text{eff}}}. \] Using the data and solving these equations, we find that the velocity of projection \(u = 10 \sqrt{2} \, \text{m/s}\).
2. A pebble is thrown horizontally from the top of a 10 m high tower with an initial velocity of \(10 \, \text{m/s}\). The air drag is negligible. The speed of the pebble when it is at the same distance from top as well as base of the tower \((g = 10 \, \text{m/s}^2)\) will be:
A. \(10\sqrt{2} \, \text{m/s}\)
B. \(10\sqrt{3} \, \text{m/s}\)
C. \(20 \, \text{m/s}\)
D. \(25 \, \text{m/s}\)
Explanation:
The pebble reaches a height of 10 m from the ground. Using conservation of energy: \[ v^2 = u^2 + 2gh. \] Substituting \(u = 10 \, \text{m/s}\), \(g = 10 \, \text{m/s}^2\), and \(h = 10 \, \text{m}\): \[ v^2 = 10^2 + 2 \cdot 10 \cdot 10 = 300 \implies v = 10\sqrt{3} \, \text{m/s}. \]
The pebble reaches a height of 10 m from the ground. Using conservation of energy: \[ v^2 = u^2 + 2gh. \] Substituting \(u = 10 \, \text{m/s}\), \(g = 10 \, \text{m/s}^2\), and \(h = 10 \, \text{m}\): \[ v^2 = 10^2 + 2 \cdot 10 \cdot 10 = 300 \implies v = 10\sqrt{3} \, \text{m/s}. \]
3. A ball is projected with velocity \(u\) at right angle to the slope which is inclined at an angle \(\theta\) with the horizontal. The distance \(x\) along the inclined plane that it will travel before striking the slope again is:
A. \(\frac{u^2}{g} \cos \theta\)
B. \(\frac{u^2}{g} \tan \theta\)
C. \(\frac{2u^2\tan \theta}{g \cos \theta }\)
D. \(\frac{u^2}{g \sin \theta \tan \theta}\)
Explanation:
Using the equations of motion, the distance \(x\) along the inclined plane is calculated as: \[ x = \frac{u^2 \sin 2\theta}{g \cos^2 \theta}. \] Simplifying further, we get: \[ x = \frac{2u^2\tan \theta}{g \cos \theta }. \]
Using the equations of motion, the distance \(x\) along the inclined plane is calculated as: \[ x = \frac{u^2 \sin 2\theta}{g \cos^2 \theta}. \] Simplifying further, we get: \[ x = \frac{2u^2\tan \theta}{g \cos \theta }. \]
4. A stone is projected at an angle \(\theta\) with the horizontal from the roof of a tall building. It falls on the ground after 3 seconds. Two seconds after the projection, it was again at the level of projection. Then the height of the building is (\(g = 10 \, \text{m/s}^2\)) :
A. \(5 \, \text{m}\)
B. \(25 \, \text{m}\)
C. \(20 \, \text{m}\)
D. \(15 \, \text{m}\)
Explanation:
The vertical motion of the stone is analyzed. At \(t = 2 \, \text{s}\), it returns to the level of projection, so the initial vertical velocity is: By using the formula of Time of flight, \[ 2u_y = g \cdot t = \frac{10 \cdot 2}{2 }= 10 \, \text{m/s}. \] Using \(H = -u_y \cdot t + \frac{1}{2} g t^2\) for \(t = 3 \, \text{s}\), we calculate: \[ H = -10 \cdot 3 + \frac{1}{2} \cdot 10 \cdot (3)^2 = -30 + 45 = 15 \, \text{m}. \]
The vertical motion of the stone is analyzed. At \(t = 2 \, \text{s}\), it returns to the level of projection, so the initial vertical velocity is: By using the formula of Time of flight, \[ 2u_y = g \cdot t = \frac{10 \cdot 2}{2 }= 10 \, \text{m/s}. \] Using \(H = -u_y \cdot t + \frac{1}{2} g t^2\) for \(t = 3 \, \text{s}\), we calculate: \[ H = -10 \cdot 3 + \frac{1}{2} \cdot 10 \cdot (3)^2 = -30 + 45 = 15 \, \text{m}. \]
5. A particle \(P\) is projected from a point on the surface of a smooth inclined plane. Simultaneously, another particle \(Q\) is released on the inclined plane from the same position. \(P\) and \(Q\) collide after \(t = 4 \, \text{s}\). The speed of projection of \(P\) is:
A. \(5 \, \text{m/s}\)
B. \(10 \, \text{m/s}\)
C. \(15 \, \text{m/s}\)
D. \(20 \, \text{m/s}\)
Explanation:
For collision to occur, the component of \(P\)'s velocity along the incline must equal the acceleration of \(Q\). The effective acceleration of \(Q\) is \(g \sin \theta\). Using:
For collision to occur, the component of \(P\)'s velocity along the incline must equal the acceleration of \(Q\). The effective acceleration of \(Q\) is \(g \sin \theta\). Using:
6. A ball is thrown from the bottom of an inclined plane at an angle \(\theta\) from the inclined surface up the plane. Another ball is thrown from a point on the inclined plane with the same speed and at the same angle \(\theta\) from the inclined surface down the plane. If the maximum heights attained by the balls with respect to the inclined surface are \(h_1\) and \(h_2\), then:
A. \(h_1 > h_2\)
B. \(h_1 < h_2\)
C. \(h_1 = h_2\)
D. All three are possible
Explanation:
The vertical component of velocity is the same for both cases. Using: \[ h = \frac{u^2 \sin^2 \theta}{2 g_{\text{eff}}}, \] since \(u\) and \(\sin^2 \theta\) are identical, \(h_1 = h_2\).
The vertical component of velocity is the same for both cases. Using: \[ h = \frac{u^2 \sin^2 \theta}{2 g_{\text{eff}}}, \] since \(u\) and \(\sin^2 \theta\) are identical, \(h_1 = h_2\).
7. Three particles \(A\), \(B\), and \(C\) are projected from the ground with the same initial speeds, making angles \(30^\circ\), \(45^\circ\), and \(60^\circ\) respectively with the horizontal. Which of the following is correct?
A. \(A\), \(B\), and \(C\) have unequal ranges
B. Ranges of \(A\) and \(C\) are equal and less than that of \(B\)
C. Ranges of \(A\) and \(C\) are equal and greater than that of \(B\)
D. All ranges are equal
Explanation:
The range formula: \[ R = \frac{u^2 \sin(2\theta)}{g}. \] For \(\theta = 30^\circ\) and \(\theta = 60^\circ\), \(\sin(60^\circ) = \sin(120^\circ)\), giving equal ranges. For \(\theta = 45^\circ\), the range is maximum.
The range formula: \[ R = \frac{u^2 \sin(2\theta)}{g}. \] For \(\theta = 30^\circ\) and \(\theta = 60^\circ\), \(\sin(60^\circ) = \sin(120^\circ)\), giving equal ranges. For \(\theta = 45^\circ\), the range is maximum.
8. A particle is projected from a point on the ground with an initial speed of \(10 \, \text{m/s}\) at an angle of \(37^\circ\) with the horizontal. At the same instant, a fly starts flying along the same path with a constant speed of \(10 \, \text{m/s}\). Then:
A. Time taken by the fly to complete the path is less than the particle
B. Acceleration of the fly is zero
C. Average velocity of both is the same for the whole journey
D. None of these
Explanation:
The fly travels in a straight path at a constant speed, while the particle follows a projectile motion. Thus, the fly takes less time to complete the journey compared to the particle.
The fly travels in a straight path at a constant speed, while the particle follows a projectile motion. Thus, the fly takes less time to complete the journey compared to the particle.
9. A ball is thrown upward at an angle of \(30^\circ\) to the horizontal and lands on the top edge of a building that is \(20 \, \text{m}\) away and \(5 \, \text{m}\) high. How fast was the ball thrown? (\(g = 10 \, \text{m/s}^2\)):
A. \(10 \, \text{m/s}\)
B. \(20 \, \text{m/s}\)
C. \(40 \, \text{m/s}\)
D. \(80 \, \text{m/s}\)
Explanation:
Using projectile motion equations for horizontal and vertical displacement: \[ x = u \cos \theta \cdot t \quad \text{and} \quad y = u \sin \theta \cdot t - \frac{1}{2} g t^2. \] Substituting \(x = 20 \, \text{m}\), \(y = 5 \, \text{m}\), \(\theta = 30^\circ\), and solving simultaneously: \[ u = 20 \, \text{m/s}. \]
Using projectile motion equations for horizontal and vertical displacement: \[ x = u \cos \theta \cdot t \quad \text{and} \quad y = u \sin \theta \cdot t - \frac{1}{2} g t^2. \] Substituting \(x = 20 \, \text{m}\), \(y = 5 \, \text{m}\), \(\theta = 30^\circ\), and solving simultaneously: \[ u = 20 \, \text{m/s}. \]
10. A particle starts from the origin at \(t = 0\) and moves in the \(x\)-\(y\) plane with constant acceleration \(a\) in the \(y\)-direction. Its equation of motion is \(y = b x^2\). The \(x\)-component of its velocity is:
A. Variable
B. \(\sqrt{\frac{b}{2a}}\)
C. \(\sqrt{\frac{b^2}{a}}\)
D. \(\sqrt{\frac{a}{2b}}\)
Explanation:
From the given equation \(y = b x^2\), differentiate to find the velocity components: \[ \frac{dy}{dt} = 2b x \cdot \frac{dx}{dt} \quad \text{and} \quad \frac{dy}{dt} = a t. \] Equating and solving for \(\frac{dx}{dt}\), we find: \[ v_x = \sqrt{\frac{a}{2b}}. \]
From the given equation \(y = b x^2\), differentiate to find the velocity components: \[ \frac{dy}{dt} = 2b x \cdot \frac{dx}{dt} \quad \text{and} \quad \frac{dy}{dt} = a t. \] Equating and solving for \(\frac{dx}{dt}\), we find: \[ v_x = \sqrt{\frac{a}{2b}}. \]
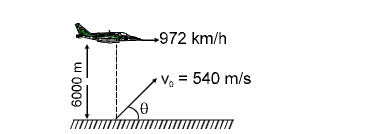
11. An aircraft moving with a speed of \(972 \, \text{km/h}\) is at a height of \(6000 \, \text{m}\), just overhead of an anti-aircraft gun. If the muzzle velocity of the gun is \(540 \, \text{m/s}\), the firing angle for the bullet to hit the aircraft should be:
A. \(73^\circ\)
B. \(30^\circ\)
C. \(60^\circ\)
D. \(45^\circ\)
Explanation:
Using relative motion and solving for the projectile motion equation, the firing angle is found to be: \[ \theta = 60^\circ. \]
Using relative motion and solving for the projectile motion equation, the firing angle is found to be: \[ \theta = 60^\circ. \]
12. A platform is pulled with a constant acceleration \(a = 5 \, \text{m/s}^2\). A particle is projected from the platform at an angle \(\theta\) with respect to the horizontal. The value of \(\tan \theta\) such that the particle returns to the starting point on the platform is: (\(g = 10 \, \text{m/s}^2\))
A. \(4\)
B. \(6\)
C. \(2\)
D. \(3\)
Explanation:
For the particle to return to the starting point, the relative horizontal displacement should be zero:
\[
\tan \theta = \frac{a}{g} = \frac{5}{10} = 2.
\]
For the particle to return to the starting point, the relative horizontal displacement should be zero:
13. The vertical height of the projectile at time \(t\) is given by \(y = 4t - 5t^2\) and the horizontal distance covered is given by \(x = 3t\). What is the angle of projection with the horizontal?
A. \(\tan^{-1}(3/5)\)
B. \(\tan^{-1}(4/5)\)
C. \(\tan^{-1}(4/3)\)
D. \(\tan^{-1}(3/4)\)
Explanation:
The vertical and horizontal velocity components are obtained by differentiating:
\[
v_y = \frac{dy}{dt} = 4 - 10t, \quad v_x = \frac{dx}{dt} = 3.
\]
At \(t = 0\), the initial velocities are:
\[
u_y = 4, \quad u_x = 3.
\]
The angle of projection is:
\[
\tan \theta = \frac{u_y}{u_x} = \frac{4}{3} \implies \theta = \tan^{-1}(4/3).
\]
The vertical and horizontal velocity components are obtained by differentiating:
14. A particle is projected from point 'A' with velocity \(u\sqrt{2}\) at an angle of \(45^\circ\) with the horizontal. It strikes the inclined plane \(BC\) at a right angle. The velocity of the particle just before the collision with the inclined plane is:
A. \(\frac{\sqrt{2}}{3}u\)
B. \(\frac{2u}{\sqrt 3}\)
C. \(u\)
D. \(\sqrt{2}u\)
Explanation:
Let the particle strike the inclined plane perpendicularly with velocity \(v\). Resolving components along and perpendicular to the incline and using kinematic equations: \[ v \cos(30^\circ) = (u\sqrt{2}) \cos(45^\circ), \] solving gives: \[ v = \frac{2u}{\sqrt 3}. \]
Let the particle strike the inclined plane perpendicularly with velocity \(v\). Resolving components along and perpendicular to the incline and using kinematic equations: \[ v \cos(30^\circ) = (u\sqrt{2}) \cos(45^\circ), \] solving gives: \[ v = \frac{2u}{\sqrt 3}. \]
15. A particle is projected from an inclined plane at an angle of \(37^\circ\) with the inclined plane in an upward direction with speed \(10 \, \text{m/s}\). The angle of the inclined plane with the horizontal is \(53^\circ\). Then the maximum height attained by the particle from the inclined plane will be:
A. \(3 \, \text{m}\)
B. \(4 \, \text{m}\)
C. \(5 \, \text{m}\)
D. Zero
Explanation:
The maximum height from the inclined plane is given by: \[ h = \frac{u^2 (\sin \theta)^2}{2 g_{\text{eff}}}, \] where \(g_{\text{eff}} = g \cos \alpha\). Substituting the values: \[ h = \frac{10^2 (\sin 37^\circ)^2}{2 \cdot 10 \cdot \cos 53^\circ} = 3 \, \text{m}. \]
The maximum height from the inclined plane is given by: \[ h = \frac{u^2 (\sin \theta)^2}{2 g_{\text{eff}}}, \] where \(g_{\text{eff}} = g \cos \alpha\). Substituting the values: \[ h = \frac{10^2 (\sin 37^\circ)^2}{2 \cdot 10 \cdot \cos 53^\circ} = 3 \, \text{m}. \]
16. Variation of displacement \(x\) of a particle moving on a straight line with time \(t\) is shown in the figure. The figure indicates:
A. The particle starts with a certain speed, but the motion is retarded.
B. The velocity of the particle is constant throughout the motion.
C. The acceleration of the particle is constant throughout the motion.
D. The particle starts with a certain speed and moves with increasing speed.
Explanation:
From the graph, the slope (velocity) is non-zero positive at \(t = 0\), but it decreases continuously and finally becomes zero. Hence, the particle starts with a certain velocity but its motion is retarded.
From the graph, the slope (velocity) is non-zero positive at \(t = 0\), but it decreases continuously and finally becomes zero. Hence, the particle starts with a certain velocity but its motion is retarded.
17. A body dropped from the top of a tower covers \(\frac{7}{16}\) of the total height in the last second of its fall. The time of fall is:
A. \(2 \, \text{s}\)
B. \(4 \, \text{s}\)
C. \(1 \, \text{s}\)
D. \(\frac{50}{7} \, \text{s}\)
Explanation:
Using the equations of motion and the given condition for the height covered in the last second:
\[
S_n = u + \frac{1}{2} g (2n - 1),
\]
substituting the conditions and solving, the total time of fall is found to be:
\[
t = 4 \, \text{s}.
\]
Using the equations of motion and the given condition for the height covered in the last second:
18. Two balls are projected from points \(A\) and \(B\) in a vertical plane. \(AB\) is a straight vertical line. The balls can collide in mid-air if \(v_1/v_2\) is equal to:
A. \(\frac{\sin \alpha}{\sin \beta}\)
B. \(\frac{\cos \beta}{\cos \alpha}\)
C. \(\frac{\tan \alpha}{\tan \beta}\)
D. \(\frac{\sin \beta}{\sin \alpha}\)
Explanation:
For the balls to collide, their relative positions must coincide. Analyzing their motion in the vertical plane and equating the horizontal components of their displacements, we get: \[ \frac{v_1}{v_2} = \frac{\cos \beta}{\cos \alpha}. \]
For the balls to collide, their relative positions must coincide. Analyzing their motion in the vertical plane and equating the horizontal components of their displacements, we get: \[ \frac{v_1}{v_2} = \frac{\cos \beta}{\cos \alpha}. \]
19. In the figure, the angle of inclination of the inclined plane is \(30^\circ\). Find the horizontal velocity \(V_0\) such that the particle hits the inclined plane perpendicularly.
A. \( V_0 = \sqrt{\frac{2gh}{5}} \)
B. \(V_0 = \sqrt{7gH}\)
C. \(V_0 = \sqrt{gH}\)
D. \(V_0 = \frac{\sqrt{gH}}{2}\)
Explanation:
For the particle to hit the inclined plane perpendicularly, the horizontal velocity component must be equal to the effective velocity component along the plane. Using the equations of motion and resolving components: \[ V_0 = \sqrt{\frac{2gh}{5}} \]
For the particle to hit the inclined plane perpendicularly, the horizontal velocity component must be equal to the effective velocity component along the plane. Using the equations of motion and resolving components: \[ V_0 = \sqrt{\frac{2gh}{5}} \]
20. A train is standing on a platform, and a man inside a compartment drops a stone. At the same instant, the train starts to move with constant acceleration. The path of the stone as seen by the person who drops it is:
A. Parabola
B. Straight line for some time and parabola for the remaining time
C. Straight line
D. Variable path that cannot be defined
Explanation:
Relative to the person in the train, the acceleration of the stone is purely downward due to gravity. The horizontal motion of the train does not influence the observed motion of the stone, so it appears as a straight line.
Relative to the person in the train, the acceleration of the stone is purely downward due to gravity. The horizontal motion of the train does not influence the observed motion of the stone, so it appears as a straight line.
Kinematics MCQ Questions with Solutions | Free Online MCQ Test
To master the principles of kinematics? Our Kinematics MCQ Online Test is designed to help students of NEET, JEE, Class 11 Physics, and even AP Physics 1. With a wide range of multiple-choice questions, detailed solutions, and explanations, this is the ultimate resource for mastering kinematics. Whether you're a student preparing for competitive exams or a teacher seeking quality content, our platform has everything you need.
Mastering Kinematics is Essential?
ematics is the backbone of physics. From understanding projectile motion in sports to analyzing vehicle dynamics, the concepts have widespread applications in science, engineering, and daily life. By practicing these MCQs, you'll build a solid foundation in one of the most fundamental areas of physics. Each question comes with a detailed explanation, ensuring students not only practice but also understand the underlying physics.
.jpeg)
.jpeg)
.png)
0 Comments